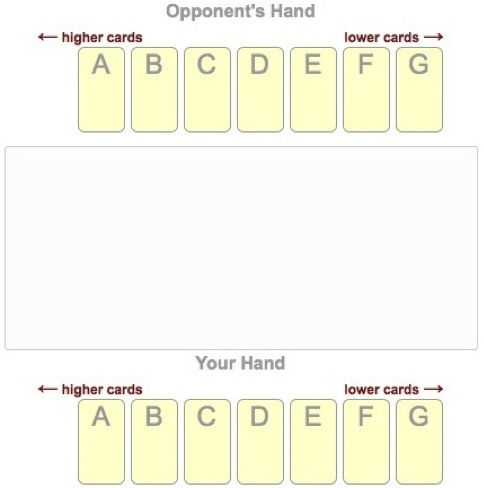
How to Win at (One-Round) War

College Mathematics Journal, September 2015.

Suppose two teams are going to play a backgammon match. The top player on team A is supposed to play the top player on team B, the #2 player is supposed to play the #2 player, etc. One team’s coach is honest, but the other is dishonest, and he decides to put his players in a different order. What is his optimal strategy, if the goal is to maximize the number of games won? If there are N players per side, what is the maximum advantage gained by cheating?

A college classmate of mine, Howard Stern, e-mailed me this problem, which he had tried and failed to solve as a graduate student back in 1980. Howard’s problem sucked me in to the point that I spent at least 100 hours working on it. It was hard but not too hard, and when I finally solved it the answer was lovely and utterly unexpected. But alas, I was only able to solve it under the assumption that there are at least 10 million players on each team. This is not very realistic!

Fortunately, the story doesn’t end there. Gary Antonick wrote about the problem in his “Numberplay” blog for the New York Times. His column, called Stern-Mackenzie One Round War (the name comes from the way I rephrased Howard’s problem as a card game similar to the children’s game of War) piqued the interest of a reader named Richard Chatwin, who improved the proof to the point where it works for all values of N. The paper above is our complete solution to Howard’s problem.

It was a total shock to me when I found out in 2017 that Howard had died a year earlier. Please click on the link here if you would like to read my tribute to him, which tells a more complete version of this story.

2184: An Absurd (and Adsurd) Tale

INTEGERS, Volume 18, paper A33 (2018)

In 2014 at the Gathering for Gardner, I heard a talk by Alex Bellos, who had just surveyed 40 thousand people to find out the world’s favorite number. No big surprise, the winning number was 7. After the talk, I thought, “What is my favorite number?” I finally settled on the number 2184, which is the difference of a number and its power in two different ways: 3^7 – 3 = 13^3 – 13 = 2184. Surely this could not be a coincidence, I thought. It demands an explanation!

I soon discovered that several people had thought about this problem before. Eight such numbers are known: 6, 30, 210, 240, 2184, 8190, 78120, and 24299970. The last example is especially remarkable: 30^5 – 30 = 4930^2 – 4930 = 24299970. I call these numbers “doubly absurd” numbers because they are a number minus its surd, or n-th root, in two different ways. It’s natural to conjecture that there are no more doubly absurd numbers. In my opinion this will not be proved for many, many years. However, I made a small amount of progress: 2184 is the only solution for which the smaller exponent is 3, the larger exponent (7, in this case) is odd, and the larger base (13, in this case) is prime.

For a witty take on this unusual property of 2184, check out Matt Parker’s video Why 1980 was a great year to be born … but 2184 will be better, which has gotten more than a million views on YouTube.

The Departed Queen

The Story Collider, December 14, 2012

This article was my attempt to write “The Old Man and the Sea” for chess. That is, I wanted to take readers who do not know anything about chess into the secret emotional and aesthetic side of the game.

Around 2002 I discovered (or rediscovered) an opening in which the player of White sacrifices his queen — the most spectacular move in chess — at an unbelievably early stage, the sixth move of the game. At first I merely tested the idea out against my computer, but in a tournament in 2006 I got the chance to spring it against a human opponent. And what an opponent! David Pruess was an International Master and one of the top 100 players in the U.S. at the time.

Yes, the article tells how I landed my fish, but it also contains reflections on what I love about chess and why computers can’t kill the game. In fact they helped me, because all the practice games against the computer helped me refine what seemed like a crazy idea into a whole philosophy of the opening.

The Tenure Chase Papers

Published in Starting Our Careers, American Mathematical Society, 1999.

In 1994, I was denied tenure at Kenyon College. The Tenure Chase Papers is my memoir of how the tenure decision happened. It’s a story with some unexpected twists and turns; if you think you know what’s going to happen (aside from what I’ve just told you), you’re probably wrong.

When I wrote the story in 1996 and posted it to the Young Mathematicians Network, I did not want it to be a woe-is-me sob story, or a vindictive score-settling. Instead, I saw it as a chance to lift the veil covering one of the most secret and mysterious rituals in an academic career, the tenure decision. How can you prepare for it? What can you do to tip the scales in your favor? How can the decision go wrong? More generally, it’s a good case study of how well-intentioned people sometimes make bad decisions… especially if they do not have access to all the information.

I think that I succeeded in my intentions, because I have probably gotten more reader feedback on this article than any other article I’ve ever written, and almost all of these readers have thanked me for writing it. Though it’s a bit dated now, I hope it will still be revealing.